...
Para ver una explicación animada de este tema, descarga el siguiente archivo:
Mínimo Común Múltiplo y Máximo Común Divisor. Para descargar haz clic aqui.
Para abrir este archivo necesitas Microsoft Power Point o Apple Computer Inc. Keynote.
Mínimo Común Múltiplo y Máximo Común Divisor
Lenguaje Algebraico (Álgebra)
El lenguaje algebraico es simplemente traducir lo que normalmente hablamos a expresiones particulares con símbolos y números. Cuando hablamos de una situación en la que necesitamos encontrar una respuesta, por todos lados escuchamos frases como esta: “lo más adecuado es escribirlo en forma de ecuación”.
La idea de esto es manipular cantidades desconocidas con símbolos fáciles de escribir. Un ejemplo muy simple es el siguiente enunciado:
Lo que gasté en dulces en la tienda fue el precio de cada dulce por el número de dulces que compré.
Escrito en Lenguaje Algebraico puede quedar de la siguiente manera:
G = P·N
Aquí G significa “lo que gasté”, P significa el "precio por dulce" y N significa "la cantidad de dulces".
Para ver una explicación animada de este tema, descarga el siguiente archivo:
Lenguaje algebraico. Para descargar haz clic aqui.
Para abrir este archivo necesitas Microsoft Power Point o Apple Computer Inc. Keynote.
Con Orgullo... Somos premiados. Muchas gracias.
Hemos Recibido de parte del Profesor Luis Parada un reconocimiento por la labor de este blog.
De parte mía y de todos mis lectores muchas gracias, estos reconocimientos nos sirven de estímulo para que todas aquellas personas que visitan nuestra bitácora tengan una mejor orientación sobre las matemáticas, y que los mensajes que por acá se colocan sirvan de reflexión y motivación en este mágico mundo de las letras y de los números.
Estos premios no son de carácter económico, sin embargo, nos sirven para aumentar la hermandad entre los blogueros y así fortalecer los lazos de amistad entre cada uno de nosotros.
Me dicen, que debo premiar a otros amigos blogueros, he decidido regresar el favor a mi amigo Luis y premiar si Blog:
123xyz_Matemáticas y algo más
Tarea 14 Mecánica de Sólidos
Tarea del tema de vigas homogéneas sometidas a flexión pura:
Ejercicios 4.4 & 4.5
b) Ahora suponga que la viga se flexiona con respecto al eje y; determine el máximo par que puede aplicarse a la viga.
Ejercicios 4.6 & 4.7
Una viga que tiene la sección mostrada está formada de una aleación de aluminio, sY = 45 ksi y sU = 70 ksi. Usando un factor de seguridad de 3,00, a) halle el máximo par que puede aplicarse a la viga cuando se flexiona con respecto al eje z.
Ahora suponga que la viga se flexiona con respecto al eje y; b) determine el máximo par que puede aplicarse a la viga.
Ejercicio 4.8
Se aplican dos fuerzas verticales a la viga con sección transversal mostrada. Halle los esfuerzos máximos de tensión y compresión en la porción BC de la viga.
Ejercicio 4.9
Se aplican dos fuerzas verticales a la viga con sección transversal mostrada. Halle los esfuerzos máximos de tensión y compresión en la porción BC de la viga.
Ejercicio 4.10
Para descargar este archivo en formato PDF haz clic aqui. (disponible hasta el 2 de mayo)
Para descargar las respuestas en formato PDF haz clic aqui. (disponible hasta el 2 de mayo)
Para ver correctamente este archivo necesitas el lector de Adobe.
Tarea 13 Mecánica de Sólidos
Tarea del tema ángulo de torsión de ejes de sección no circular:
Ejercicios 3.112, 3.113, 3.114 & 3.115
Cada una de las tres barras de acero, mostradas en la siguiente figura, está sometida a un torque de magnitud T = 275 N·m. Sabiendo que el esfuerzo cortante admisible es de 50 MPa, halle: a) la dimensión b requerida en cada barra.
Cada una de las tres barras, mostradas a continuación, está sometida a un torque de 5 kips·pulg. Si el cortante admisible es de 8 ksi, halle: b) la dimensión b requerida de cada barra.
Cada una de las tres barras de Aluminio, que se muestran en la siguiente figura, debe ser sometida a torsión en un ángulo de 1,25º. Sabiendo que b = 1,5 pulg, tadm = 7,5 ksi y G = 3,7´106 psi, halle: c) la longitud mínima admisible de cada barra.
Cada una de las tres barras de Aluminio, que a continuación se muestran, debe ser sometida a torsión en un ángulo de 2º. Sabiendo que b = 30 mm, tadm = 50 MPa y G = 26 GPa, halle: d) la longitud mínima admisible de cada barra.
Ejercicios 3.116, 3.117, 3.118 & 3.119
Los ejes A y B son del mismo material y tienen la misma área transversal, pero A es de sección circular y B de sección cuadrada. Determine la relación de los esfuerzos cortantes máximos que ocurren en A y B, respectivamente, cuando los dos ejes están sometidos al mismo torque (TA = TB). Suponga que ambas deformaciones son elásticas.
Los ejes A y B son del mismo material y tienen igual longitud e igual área transversal, pero A es de sección circular y B de sección cuadrada. Determine la relación de los torques máximos TA y TB que pueden aplicarse sin peligro a A y B, respectivamente.
Los ejes A y B son del mismo material y tienen igual longitud e igual área transversal, pero A tiene sección transversal circular y B tiene sección cuadrada. Halle la relación entre los ángulos máximos de torsión fA y fB a que pueden someterse los ejes sin peligro.
Los ejes A y B son del mismo material y tienen igual longitud e igual área transversal, pero A es de sección circular y B de sección cuadrada. Determine la relación de los ángulos de torsión fA y fB cuando se somete a los dos ejes al mismo torque (TA = TB). Suponga que ambas deformaciones son elásticas.
Para descargar este archivo en formato MS Word haz clic aquí. (disponible hasta el 18 de abril)
Para ver correctamente este archivo necesitas el Micro Soft Office u Open Office Gratuito.
Para descargar este archivo en formato PDF haz clic aqui. (disponible hasta el 18 de abril)
Para descargar las respuestas en formato PDF haz clic aqui. (disponible hasta el 18 de abril)
Para ver correctamente este archivo necesitas el lector de Adobe.
Tarea 12 de Mecánica de Sólidos
Tarea del tema de Ejes de Transmisión de Potencia:
Ejercicios 3.62 & 3.63
Cuando un eje hueco gira a 180 rpm, un estroboscopio indica que el ángulo de torsión es 3º. Sabiendo que G = 77 GPa, determine: a) la potencia transmitida, b) el máximo esfuerzo cortante en el eje. Las dimensiones del eje se muestran en la siguiente figura.
El eje hueco, mostrado en la figura anterior (G = 77 GPa, tadm = 50 MPa) gira a 240 rpm. Determine: c) la potencia máxima que puede transmitirse, d) el correspondiente ángulo de torsión del eje.
Ejercicio 3.64
Un eje motor hueco de acero (G = 11,2x106 psi) tiene 8 pie de longitud y sus diámetros exterior e interior son 2,50 y 2,25 pulg, respectivamente. Sabiendo que el eje transmite 200 hp a 1500 rpm, determine: a) el máximo esfuerzo cortante, b) el ángulo de torsión del eje.
Ejercicio 3.65
Sabiendo que G = 11,2x106 psi y tadm = 6000 psi para el acero que se va a utilizar, determine: a) el menor diámetro admisible de un eje sólido que debe transmitir 18 hp a 2400 rpm, b) el correspondiente ángulo de torsión en una longitud de 6 pie en el eje.
Ejercicios 3.66 & 3.67
Los dos ejes sólidos y los engranajes mostrados en la figura anterior se usan para transmitir 12 kW del motor en A, que gira a 20 Hz, a una máquina herramienta en D. Sabiendo que el esfuerzo cortante admisible máximo es 60 MPa para cada eje, halle el diámetro: c) del eje AB, d) del eje CD.
Para descargar este archivo en formato MS Word haz clic aquí. (disponible hasta el 15 de abril)
Para ver correctamente este archivo necesitas el Micro Soft Office u Open Office Gratuito.
Para descargar este archivo en formato PDF haz clic aqui. (disponible hasta el 15 de abril)
Para descargar las respuestas en formato PDF haz clic aqui. (disponible hasta el 15 de abril)
Para ver correctamente este archivo necesitas el lector de Adobe.
Tarea 11 de Mecánica de Sólidos
Tarea del tema de Torsión de Ejes Estáticamente Indeterminados:
Ejercicios 3.45 & 3.46
Dos ejes sólidos de acero (G = 11,2x106 psi) están conectados a un disco de acople B y a soportes fijos en A y C. Para la carga mostrada en la siguiente figura, determine: a) la reacción en cada soporte, b) el máximo esfuerzo cortante en AB, c) el máximo esfuerzo cortante en BC.
Ahora suponga que el eje AB se reemplaza por uno hueco del mismo diámetro exterior y 1 pulg de diámetro interior, determine: d) la reacción en cada soporte, e) el máximo esfuerzo cortante en AB, f) el máximo esfuerzo cortante en BC.
Ejercicios 3.47 & 3.48
Los cilindros AB y BC están unidos en B, y en A y C a soportes fijos. Sabiendo que AB es de Aluminio (G = 26 GPa) y BC de Latón (G = 39 GPa), halle para la carga mostrada en la siguiente figura: a) La reacción en cada soporte, b) el máximo esfuerzo cortante en AB, c) el máximo esfuerzo cortante en BC.
Ahora suponga que AB es de acero (G = 77 GPa) en lugar de Aluminio, halle para la carga mostrada en la siguiente figura: d) La reacción en cada soporte, e) el máximo esfuerzo cortante en AB, f) el máximo esfuerzo cortante en BC.
Ejercicios 3.49 & 3.50
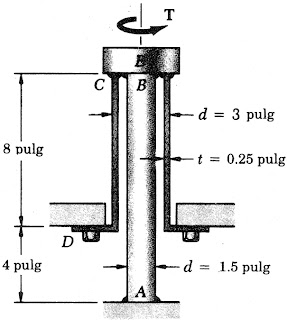
El eje sólido AB y la camisa CD están ambos unidos al cilindro corto E. El eje de acero AB tiene un Gs = 11,2x106 psi y (tadm)s = 12 ksi, mientras la camisa de latón CD tiene un Gb = 5,6x106 psi y (tadm)b = 7 ksi. Halle el máximo torque que puede aplicarse al cilindro E mostrado en la siguiente figura.
Si se aplica un torque T de 20 kips·pulg al cilindro E de la figura mostrada a continuación, Determine: a) el esfuerzo cortante máximo en el eje AB, b) el cortante máximo en la camisa CD.
Para descargar este archivo en formato MS Word haz clic aquí. (disponible hasta el 9 de abril)
Para ver correctamente este archivo necesitas el Micro Soft Office u Open Office Gratuito.
Para descargar este archivo en formato PDF haz clic aqui.
Para ver correctamente este archivo necesitas el lector de Adobe.
Suscribirse a:
Entradas (Atom)
