Tarea 15 Mecánica de Sólidos

Tarea del tema de vigas compuestas de 2 materiales diferentes sometidas a flexión pura:

Ejercicio 4.35

Dos barras de latón y dos de aluminio están soldadas para formar el elemento compuesto, tal como se muestra en la figura. Usando los datos dados halle el máximo momento admisible cuando se flexiona el elemento con respecto al eje horizontal.

Módulo de Elasticidad del Aluminio: 70 GPa

Módulo de Elasticidad delLatón: 105 GPa

Esfuerzo admisible del Aluminio: 100 MPa

Esfuerzo admisible del Latón: 160 MPa

Ejercicios 4.36 & 4.37

Dos barras de latón y dos de aluminio están soldadas para formar el elemento compuesto, tal como se muestra en la figura. Usando los datos dados halle el máximo momento admisible cuando se flexiona el elemento con respecto al eje horizontal.

Módulo de Elasticidad del Aluminio: 70 GPa

Módulo de Elasticidad del Latón: 105 GPa

Esfuerzo admisible del Aluminio: 100 MPa

Esfuerzo admisible del Latón: 160 MPa

Para el elemento compuesto anterior halle el máximo momento admisible cuando se flexiona con respecto a un eje vertical.

Ejercicios 4.38 & 4.39

Se ha reforzado la viga de madera de 6 x 10 pulgadas poniéndole dos platinas de acero, tal como se muestra en la siguiente figura. Usando los datos dados abajo, halle el máximo momento flector admisible cuando se flexiona con respecto al eje horizontal.

Módulo de Elasticidad de la Madera: 1,9 x 10⁶ psi

Módulo de Elasticidad del Acero: 29 x 10⁶ psi

Esfuerzo admisible de la Madera: 1800 psi

Esfuerzo admisible del Acero: 24 ksi

Para el elemento compuesto anterior, halle el máximo momento flector cuando se flexiona el elemento con respecto a un eje vertical.

Para descargar este archivo en formato WORD haz clic aqui. (disponible hasta el 16 de mayo)

Para ver correctamente este archivo necesitas el MicroSoft Word 2000 o posterior.

Para descargar este archivo en formato PDF haz clic aqui. (disponible hasta el 16 de mayo)

Para descargar las respuestas en formato PDF haz clic aqui. (disponible hasta el 16 de mayo)

Para ver correctamente este archivo necesitas el lector de Adobe.

Mínimo Común Múltiplo y Máximo Común Divisor

...

Para ver una explicación animada de este tema, descarga el siguiente archivo:

Mínimo Común Múltiplo y Máximo Común Divisor. Para descargar haz clic aqui.

Para abrir este archivo necesitas Microsoft Power Point o Apple Computer Inc. Keynote.

Lenguaje Algebraico (Álgebra)

El lenguaje algebraico es simplemente traducir lo que normalmente hablamos a expresiones particulares con símbolos y números. Cuando hablamos de una situación en la que necesitamos encontrar una respuesta, por todos lados escuchamos frases como esta: “lo más adecuado es escribirlo en forma de ecuación”.

La idea de esto es manipular cantidades desconocidas con símbolos fáciles de escribir. Un ejemplo muy simple es el siguiente enunciado:

Lo que gasté en dulces en la tienda fue el precio de cada dulce por el número de dulces que compré.

Escrito en Lenguaje Algebraico puede quedar de la siguiente manera:

G = P·N

Aquí G significa “lo que gasté”, P significa el "precio por dulce" y N significa "la cantidad de dulces".

Para ver una explicación animada de este tema, descarga el siguiente archivo:

Lenguaje algebraico. Para descargar haz clic aqui.

Para abrir este archivo necesitas Microsoft Power Point o Apple Computer Inc. Keynote.

Con Orgullo... Somos premiados. Muchas gracias.

Hemos Recibido de parte del Profesor Luis Parada un reconocimiento por la labor de este blog.

De parte mía y de todos mis lectores muchas gracias, estos reconocimientos nos sirven de estímulo para que todas aquellas personas que visitan nuestra bitácora tengan una mejor orientación sobre las matemáticas, y que los mensajes que por acá se colocan sirvan de reflexión y motivación en este mágico mundo de las letras y de los números.



Estos premios no son de carácter económico, sin embargo, nos sirven para aumentar la hermandad entre los blogueros y así fortalecer los lazos de amistad entre cada uno de nosotros.



Me dicen, que debo premiar a otros amigos blogueros, he decidido regresar el favor a mi amigo Luis y premiar si Blog:

123xyz_Matemáticas y algo más

Tarea 14 Mecánica de Sólidos

Tarea del tema de vigas homogéneas sometidas a flexión pura:

Ejercicios 4.4 & 4.5

La viga de acero mostrada está hecha de un acero con s_Y = 250 MPa y s_U = 400 MPa. Usando un factor de seguridad de 2,50, a) determine el máximo par que puede aplicarse a la viga cuando se flexiona con respecto al eje z.

b) Ahora suponga que la viga se flexiona con respecto al eje y; determine el máximo par que puede aplicarse a la viga.

Ejercicios 4.6 & 4.7

Una viga que tiene la sección mostrada está formada de una aleación de aluminio, s_Y = 45 ksi y s_U = 70 ksi. Usando un factor de seguridad de 3,00, a) halle el máximo par que puede aplicarse a la viga cuando se flexiona con respecto al eje z.

Ahora suponga que la viga se flexiona con respecto al eje y; b) determine el máximo par que puede aplicarse a la viga.

Ejercicio 4.8

Se aplican dos fuerzas verticales a la viga con sección transversal mostrada. Halle los esfuerzos máximos de tensión y compresión en la porción BC de la viga.

Ejercicio 4.9

Se aplican dos fuerzas verticales a la viga con sección transversal mostrada. Halle los esfuerzos máximos de tensión y compresión en la porción BC de la viga.

Ejercicio 4.10

Se aplican dos fuerzas verticales a la viga con sección transversal mostrada. Halle los esfuerzos máximos de tensión y compresión en la porción BC de la viga.

Para descargar este archivo en formato PDF haz clic aqui. (disponible hasta el 2 de mayo)


Para descargar las respuestas en formato PDF haz clic aqui. (disponible hasta el 2 de mayo)


Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 13 Mecánica de Sólidos

Tarea del tema ángulo de torsión de ejes de sección no circular:

Ejercicios 3.112, 3.113, 3.114 & 3.115

Cada una de las tres barras de acero, mostradas en la siguiente figura, está sometida a un torque de magnitud T = 275 N·m. Sabiendo que el esfuerzo cortante admisible es de 50 MPa, halle: a) la dimensión b requerida en cada barra.

Cada una de las tres barras, mostradas a continuación, está sometida a un torque de 5 kips·pulg. Si el cortante admisible es de 8 ksi, halle: b) la dimensión b requerida de cada barra.

Cada una de las tres barras de Aluminio, que se muestran en la siguiente figura, debe ser sometida a torsión en un ángulo de 1,25º. Sabiendo que b = 1,5 pulg, t_adm = 7,5 ksi y G = 3,7´10⁶ psi, halle: c) la longitud mínima admisible de cada barra.

Cada una de las tres barras de Aluminio, que a continuación se muestran, debe ser sometida a torsión en un ángulo de 2º. Sabiendo que b = 30 mm, t_adm = 50 MPa y G = 26 GPa, halle: d) la longitud mínima admisible de cada barra.

Ejercicios 3.116, 3.117, 3.118 & 3.119

Los ejes A y B son del mismo material y tienen la misma área transversal, pero A es de sección circular y B de sección cuadrada. Determine la relación de los esfuerzos cortantes máximos que ocurren en A y B, respectivamente, cuando los dos ejes están sometidos al mismo torque (T_A = T_B). Suponga que ambas deformaciones son elásticas.

Los ejes A y B son del mismo material y tienen igual longitud e igual área transversal, pero A es de sección circular y B de sección cuadrada. Determine la relación de los torques máximos T_A y T_B que pueden aplicarse sin peligro a A y B, respectivamente.

Los ejes A y B son del mismo material y tienen igual longitud e igual área transversal, pero A tiene sección transversal circular y B tiene sección cuadrada. Halle la relación entre los ángulos máximos de torsión f_A y f_B a que pueden someterse los ejes sin peligro.

Los ejes A y B son del mismo material y tienen igual longitud e igual área transversal, pero A es de sección circular y B de sección cuadrada. Determine la relación de los ángulos de torsión f_A y f_B cuando se somete a los dos ejes al mismo torque (T_A = T_B). Suponga que ambas deformaciones son elásticas.

Para descargar este archivo en formato MS Word haz clic aquí. (disponible hasta el 18 de abril)


Para ver correctamente este archivo necesitas el Micro Soft Office u Open Office Gratuito.



Para descargar este archivo en formato PDF haz clic aqui. (disponible hasta el 18 de abril)


Para descargar las respuestas en formato PDF haz clic aqui. (disponible hasta el 18 de abril)


Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 12 de Mecánica de Sólidos

Tarea del tema de Ejes de Transmisión de Potencia:

Ejercicios 3.62 & 3.63

Cuando un eje hueco gira a 180 rpm, un estroboscopio indica que el ángulo de torsión es 3º. Sabiendo que G = 77 GPa, determine: a) la potencia transmitida, b) el máximo esfuerzo cortante en el eje. Las dimensiones del eje se muestran en la siguiente figura.

El eje hueco, mostrado en la figura anterior (G = 77 GPa, t_adm = 50 MPa) gira a 240 rpm. Determine: c) la potencia máxima que puede transmitirse, d) el correspondiente ángulo de torsión del eje.

Ejercicio 3.64

Un eje motor hueco de acero (G = 11,2x10⁶ psi) tiene 8 pie de longitud y sus diámetros exterior e interior son 2,50 y 2,25 pulg, respectivamente. Sabiendo que el eje transmite 200 hp a 1500 rpm, determine: a) el máximo esfuerzo cortante, b) el ángulo de torsión del eje.

Ejercicio 3.65

Sabiendo que G = 11,2x10⁶ psi y t_adm = 6000 psi para el acero que se va a utilizar, determine: a) el menor diámetro admisible de un eje sólido que debe transmitir 18 hp a 2400 rpm, b) el correspondiente ángulo de torsión en una longitud de 6 pie en el eje.

Ejercicios 3.66 & 3.67

Dos ejes sólidos y dos engranajes (mostrados en la siguiente figura) se utilizan para transmitir 12 kW del motor en A, que gira a 20 Hz, a una máquina herramienta en D. Sabiendo que cada eje tiene 25 mm de diámetro, halle el esfuerzo cortante máximo: a) en el eje AB, b) en el eje CD.

Los dos ejes sólidos y los engranajes mostrados en la figura anterior se usan para transmitir 12 kW del motor en A, que gira a 20 Hz, a una máquina herramienta en D. Sabiendo que el esfuerzo cortante admisible máximo es 60 MPa para cada eje, halle el diámetro: c) del eje AB, d) del eje CD.

Para descargar este archivo en formato MS Word haz clic aquí. (disponible hasta el 15 de abril)

Para ver correctamente este archivo necesitas el Micro Soft Office u Open Office Gratuito.



Para descargar este archivo en formato PDF haz clic aqui. (disponible hasta el 15 de abril)

Para descargar las respuestas en formato PDF haz clic aqui. (disponible hasta el 15 de abril)

Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 11 de Mecánica de Sólidos

Tarea del tema de Torsión de Ejes Estáticamente Indeterminados:

Ejercicios 3.45 & 3.46

Dos ejes sólidos de acero (G = 11,2x10⁶ psi) están conectados a un disco de acople B y a soportes fijos en A y C. Para la carga mostrada en la siguiente figura, determine: a) la reacción en cada soporte, b) el máximo esfuerzo cortante en AB, c) el máximo esfuerzo cortante en BC.

Ahora suponga que el eje AB se reemplaza por uno hueco del mismo diámetro exterior y 1 pulg de diámetro interior, determine: d) la reacción en cada soporte, e) el máximo esfuerzo cortante en AB, f) el máximo esfuerzo cortante en BC.

Ejercicios 3.47 & 3.48

Los cilindros AB y BC están unidos en B, y en A y C a soportes fijos. Sabiendo que AB es de Aluminio (G = 26 GPa) y BC de Latón (G = 39 GPa), halle para la carga mostrada en la siguiente figura: a) La reacción en cada soporte, b) el máximo esfuerzo cortante en AB, c) el máximo esfuerzo cortante en BC.

Ahora suponga que AB es de acero (G = 77 GPa) en lugar de Aluminio, halle para la carga mostrada en la siguiente figura: d) La reacción en cada soporte, e) el máximo esfuerzo cortante en AB, f) el máximo esfuerzo cortante en BC.

Ejercicios 3.49 & 3.50

El eje sólido AB y la camisa CD están ambos unidos al cilindro corto E. El eje de acero AB tiene un G_s = 11,2x10⁶ psi y (t_adm)_s = 12 ksi, mientras la camisa de latón CD tiene un G_b = 5,6x10⁶ psi y (t_adm)_b = 7 ksi. Halle el máximo torque que puede aplicarse al cilindro E mostrado en la siguiente figura.

Si se aplica un torque T de 20 kips·pulg al cilindro E de la figura mostrada a continuación, Determine: a) el esfuerzo cortante máximo en el eje AB, b) el cortante máximo en la camisa CD.

Para descargar este archivo en formato MS Word haz clic aquí. (disponible hasta el 9 de abril)

Para ver correctamente este archivo necesitas el Micro Soft Office u Open Office Gratuito.



Para descargar este archivo en formato PDF haz clic aqui.

Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 9 & 10 Mecánica de Sólidos

Tarea del tema de Torsión:

Ejercicios 3.1 & 3.24

a) Halle el máximo esfuerzo cortante causado por un torque de 40 kips·pulg en el eje sólido de Aluminio de 3 pulg de diámetro, que se muestra a continuación. b) Resuelva el inciso “a” suponiendo que el eje se ha reemplazado por uno hueco con el mismo diámetro exterior y 1 pulg de diámetro interior.

c) Determine el ángulo de torsión causado por un torque T de 40 kips·pulg en el eje de Aluminio de 3 pulg de diámetro, que se muestra en la siguiente figura (G = 3,7x10⁶ psi). d) Resuelva el inciso anterior suponiendo que se ha reemplazado el eje sólido por un eje hueco con el mismo diámetro exterior y 1 pulg de diámetro interior.

Ejercicios 3.2 & 3.23

a) Halle el torque T que causa un cortante máximo de 45 MPa en el eje cilíndrico hueco mostrado a continuación. b) halle el mismo esfuerzo cortante causado por el mismo torque en un eje sólido con la misma área transversal.

c) Halle el torque T que da origen a un ángulo de torsión de 3º en el cilindro hueco de acero mostrado en la siguiente figura (G = 77 GPa). d) Determine el ángulo de torsión producido por el mismo torque T en un eje cilíndrico sólido del mismo material y con la misma sección transversal.

Ejercicios 3.3

Se aplica un torque de 1,75 kN·m al cilindro sólido de la figura mostrada a continuación. Halle: a) el cortante máximo, b) el porcentaje del torque tomado por el núcleo de 25 mm de diámetro.

Ejercicios 3.4

a) Halle el torque que debe aplicarse al eje sólido de 3 pulg de diámetro sin exceder un cortante admisible de 12 ksi. b) Resuelva el inciso “a” suponiendo que al eje sólido lo reemplaza un eje hueco de igual área y cuyo diámetro interior equivale a la mitad del exterior.

Ejercicios 3.5 & 3.27

Los torques mostrados en la siguiente figura, se ejercen sobre las poleas A, B y C. Si ambos ejes son sólidos, halle el máximo esfuerzo cortante: a) en el eje AB, b) en el eje BC.

Los torques que se ilustran en la siguiente figura se ejercen sobre las poleas A, B y C. Sabiendo que ambos ejes son sólidos y hechos de Latón (G = 39 GPa), halle en ángulo de torsión entre: c) A y B, d) A y C.

Ejercicios 3.6 & 3.7

En condiciones normales de aplicación, el motor eléctrico, que se muestra a continuación, ejerce un torque de 12 kips·pulg sobre E. Sabiendo que cada eje es sólido, halle el máximo esfuerzo cortante: a) en el eje BC, b) en el eje CD, c) en el eje DE.

Ahora suponga que se ha perforado un hueco de 1 pulg de diámetro en cada eje, halle el máximo esfuerzo cortante: d) en el eje BC, e) en el eje CD, f) en el eje DE.

Ejercicios 3.8

Los torques mostrados en la siguiente figura, se ejercen sobre las poleas A, B, C y D. Sabiendo que los ejes son sólidos, halle: a) el eje en el cual ocurre el máximo esfuerzo cortante, b) la magnitud de dicho esfuerzo.

Ejercicios 3.25

Halle el máximo diámetro admisible de una barra de acero de 10 pie de longitud (G = 11,2x10⁶ psi), si la barra ha de ser sometida a un ángulo de torsión de 90º sin que exceda un esfuerzo cortante de 15 ksi.

Ejercicios 3.26

Mientras un pozo de petróleo está siendo perforado a 2 500 m de profundidad se observa que el tope de la tubería perforadora que se utiliza, de 200 mm de diámetro, de acero (G = 77 GPa), rota 2,5 revoluciones antes que la punta perforadora empiece a operar. Halle el esfuerzo cortante máximo que causa la torsión en la tubería.

Ejercicios 3.28 & 3.29

El motor eléctrico, mostrado en la figura siguiente, ejerce un torque de 6 kips·pulg sobre el eje de Aluminio ABCD cuando rota a velocidad constante. Sabiendo que G = 3,7x10⁶ psi y que los torques ejercidos sobre las poleas B y C son los indicados en la figura, halle el ángulo de torsión entre: a) B y C, b) B y D.

Ahora suponga que se ha perforado un hueco de 1 pulg de diámetro en todo el eje, halle el ángulo de torsión entre: c) B y C, d) B y D.

Ejercicios 3.30

Los torques mostrados en la siguiente figura, se ejercen en las poleas A, B, C y D. Si cada eje es sólido, de 120 mm de longitud y hecho de acero (G = 77 GPa), halle el ángulo de torsión entre: a) A y C, b) A y E.

Ejercicios 3.31 & 3.32

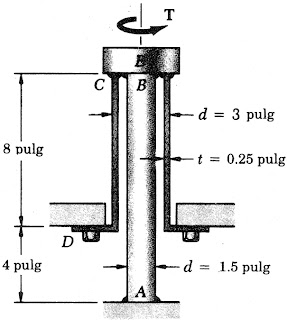
El eje sólido AB tiene un diámetro d_s = 1,5 pulg y está hecho de acero con G = 11,2x10⁶ psi, y t_adm = 12 ksi, en tanto que la camisa CD es de Latón con G = 5,6x10⁶ psi, y t_adm = 7 ksi. Halle a) el ángulo máximo que puede girarse el extremo A.

El eje sólido AB tiene un diámetro d_s = 1,75 pulg y está hecho de acero con G = 11,2x10⁶ psi, y t_adm = 12 ksi, en tanto que la camisa CD es de Latón con G = 5,6x10⁶ psi, y t_adm = 7 ksi. Halle: b) el máximo torque T que puede aplicarse en A si no deben excederse los esfuerzos admisibles dados y si el ángulo de torsión de la camisa CD no debe pasar de 0,375º. c) el ángulo de rotación correspondiente del extremo A.

Para descargar este archivo en formato MS Word haz clic aquí. (disponible hasta el 4 de abril)



Para ver correctamente este archivo necesitas el Micro Soft Office u Open Office Gratuito.



Para descargar este archivo en formato PDF haz clic aquí.



Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 8 Mecánica de Sólidos

Tarea del tema de Deformaciones cortantes:

Ejercicios 2.82 & 2.83

Una unidad de aislamiento vibratorio consta de 2 bloques de caucho endurecido adheridos a una placa AB y a soportes rígidos como se muestra en la siguiente figura. Sabiendo que una fuerza P = 6 kips causa una deflexión d = 1/16 pulg de la placa AB, halle el módulo de rigidez del caucho usado.

Una unidad de aislamiento vibratorio consta de 2 bloques de caucho endurecido con un módulo de rigidez G = 2.75 ksi adheridos a una placa AB y a soportes rígidos, como se muestra en la figura anterior. Llamando P a la magnitud de la fuerza aplicada en la placa y d a la deflexión correspondiente, halle la constante de resorte efectiva P/d del sistema.

Ejercicios 2.84 & 2.85

El bloque plástico mostrado en la siguiente figura está pegado al soporte rígido y a una placa vertical, a la cual se aplica una fuerza P de 240 kN. Sabiendo que para el plástico utilizado G = 1050 MPa, halle a) la deflexión de la placa; b) La carga P que debe aplicarse para producir una deflexión de 1.5 mm.

Ejercicios 2.86 & 2.87

Dos bloques de caucho con G = 1.75 ksi están adheridos a soportes rígidos y a una placa AB, como se muestra en la siguiente figura. Sabiendo que c = 4 pulg y P = 10 kips, halle las dimensiones mínimas admisibles a y b de los bloques si el cortante en el caucho no debe pasar de 200 psi y la deflexión de la placa debe ser al menos 0.1 pulg.

Dos bloques de caucho con G = 1.50 ksi están adheridos a soportes rígidos y a una placa AB, como se muestra en la figura anterior. Sabiendo que b = 8 pulg y c = 5 pulg, determine la máxima carga admisible P y el espesor mínimo admisible a de los bloques si el cortante en el caucho no debe pasar de 210 psi y la deflexión de la placa debe ser de por lo menos de ¼ pulg.

Para descargar este archivo en formato PDF haz clic aquí.


Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 7 Mecánica de Sólidos

Tarea del tema de Relación de Poisson:



Ejercicios 2.66 & 2.67

En una Prueba de Tensión se somete una barra de Aluminio de 20 mm de diámetro a una fuerza de tensión P = 30 kN. Sabiendo que E = 70 GPa, y n = 0.35, determine a) el alargamiento de la barra en una longitud de 150 mm, b) el cambio en el diámetro de la barra.

En una prueba normalizada de tensión se somete una barra de plástico experimental de 20 mm de diámetro a una fuerza P = 6 kN. Sabiendo que se detecta una alargamiento de 14 mm y una disminución en el diámetro de 0.85 mm en una longitud de medición de 150 mm, determine el módulo de elasticidad, el de rigidez y la relación de Poisson del material.

Ejercicio 2.68


Una línea con pendiente 4:10 fue grabada en una placa de Latón amarillo de 6 pulg de ancho y ¼ pulg de espesor. Usando los datos del Apéndice B, halle la pendiente de la línea cuando la placa esté sometida a una fuerza axial de 45 kips, como se muestra a continuación.

Ejercicio 2.69


Una tubería de acero de 6 pies de longitud, 12 pulg de diámetro exterior y ½ pulg de espesor, se usa como columna corta para soportar una carga axial de 300 kips. Usando los datos del Apéndice B para el acero estructural, halle a) el cambio de longitud de la tubería, b) el cambio de diámetro exterior, c) el cambio de espesor de la tubería.

Para descargar este archivo en formato PDF haz clic aquí.


Para descargar el Apéndice B formato PDF haz clic aquí.


Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 6 Mecánica de Sólidos

Tarea del tema de Problemas Estáticamente Indeterminados:

Ejercicio 2.33

Un poste de concreto (mostrado en la figura siguiente) de 4 pies está reforzado con 4 barras de acero de ¾ pulg de diámetro. Si E_s = 29 x 10⁶ psi y E_c = 3.6 x 10⁶ psi, halle los esfuerzos normales en el acero y en el concreto cuando se aplica al poste una carga axial de 150 kips.

Ejercicios 2.34 & 2.35

Una barra de 250 mm con seción de 15 x 30 mm consta de 2 capas de Aluminio de 5 mm, unidas a una central de Latón del mismo espesor. Si se le somete a cargas axiales P = 30 kN y sabiendo que E_Al = 70 GPa y E_L = 105 GPa, halle el esfuerzo normal a) en el Aluminio, b) en el Latón y c) el alargamiento de la barra compuesta si la carga axial P es de 45 kN.

Ejercicio 2.36

Se aplican fuerzas de compresión de 40 kips, axiales, a ambos extremos del conjunto mostrado a continuación, por medio de platinas rígidas terminales. Sabiendo que E_s = 29 x 10⁶ psi y E_a = 10 x 10⁶ psi, halle: a) los esfuerzos normales en el núcleo de Acero y en la cubierta de Aluminio, b) la deformación del conjunto.

Ejercicio 2.37

Una barra de plástico que consta de dos partes cilíndricas AB y BC está restringida en ambos extremos y soporta cargas de 6 kips, como las mostradas en la siguiente figura. Sabiendo que E = 0.45 x 10⁶ psi, halle: a) las reacciones en A y C, b) el esfuerzo normal en cada porción de la barra.

Ejercicios 2.38 & 2.39

Dos barras cilíndricas, una de Acero y la otra de Latón, están unidas en C y tienen soportes rígidos en A y E. Dada la Carga mostrada en la siguiente figura y sabiendo que E_s = 200 GPa y Eb = 105 GPa, halle: a) las reacciones en A y en E, b) la deflexión del punto C.

Ahora suponga que la barra AC es de Latón y la barra CE es de Acero, halle: c) las reacciones en A y en E, d) la deflexión del punto C.

Para descargar este archivo en formato PDF haz clic aquí.


Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 5 Mecánica de Sólidos

DIAGRAMA ESFUERZO-DEFORMACIÓN INGENIERIL

El Diagrama Esfuerzo-Deformación Ingenieril es una herramienta muy útil para determinar muchas de las características mecánicas de los materiales. Este diagrama se obtiene al someter un material a un Ensayo de Tensión Uniaxial. El material a ensayar debe presentarse en una configuración apropiada a la que se llama Espécimen o probeta de tensión uniaxial. El siguiente es un diagrama típico de Escuerzo-Deformación para un material elástico lineal que presenta un comportamiento plástico después del elástico, relacionado con la ductilidad del material.

Del diagrama Esfuerzo-Deformación Ingenieril se pueden obtener las siguientes propiedades de los materiales: Módulo elástico o de Young (E), Esfuerzo de Cedencia (s_Y), la resistencia a la Tensión o esfuerzo último (s_U), la deformación máxima (e_max), la resiliencia (área bajo la curva de la región elástica), Tenacidad (área bajo la curva del diagrama total), etc.

Para descargar el documento completo (que contiene la tarea 5) formato PDF haz clic aquí.



Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 4 Mecánica de Sólidos

Tarea del tema de deformaciones normales:

Ejercicio 2.1

Una barra de polietileno de 12 pulg de largo y diámetro de 0.5 pulg es sometida a una tensión de 800 lb. Si E=0.45x10⁶ psi, halle: a) el alargamiento de la barra, b) el esfuerzo normal.

Ejercicio 2.2

Un alambre de acero de 60 m no se debe estirar más de 48 mm cuando la tensión en el alambre es de 6 kN. Si E=200 GPa, halle: a) el diámetro mínimo que puede escogerse para el alambre, b) el valor correspondiente del esfuerzo normal

Ejercicio 2.3

Un alambre de acero, E=200 GPa, con una longitud de 80 m y 5 mm de diámetro, tiene un esfuerzo último de tensión de 400 MPa. Si se desea un Factor de Seguridad de 3.2, ¿Cuál es: a) la mayor tensión admisible en el alambre, b) el alargamiento correspondiente del mismo?

Ejercicio 2.4

Un hilo de Nylon es sometido a 2 lb de tensión. Si E=0.5x10⁶ psi y el máximo esfuerzo normal admisible es de 6 ksi, determine: a) el diámetro requerido de hilo, b) el porcentaje de incremento en la longitud del hilo.

Ejercicio 2.5

Una barra de control hecha de Latón debe alargarse 1/8 pulg con una carga de 900 lb. Si E=15x10⁶ psi y el máximo esfuerzo normal admisible es de 60 ksi, halle: a) el menor diámetro que puede tener la barra, b) la longitud correspondiente requerida de la barra.

Ejercicio 2.6

Un alambre de Aluminio de 4 mm de diámetro se alarga 25 mm cuando la tensión es 400 N. Sabiendo que E=70 GPa y la resistencia última de tensión es de 110 MPa, halle: a) la longitud del alambre, b) el Factor de Seguridad.

Ejercicio 2.7

Una barra de Aluminio de 1.5 m de largo no debe alargarse más de 1 mm ni el esfuerzo normal pasar de 40 MPa cuando la barra está sometida a una fuerza axial de 3 kN. Si E=70 GPa, halle el diámetro requerido de la barra.

Ejercicio 2.8

Se debe someter un hilo de Nylon a una tensión de 2.5 lb. Sabiendo que E=0.5x10⁶ psi, que el esfuerzo normal máximo es 6 ksi y que la longitud del hilo no debe aumentar más del 1%, halle el diámetro requerido.



Para descargar este archivo en formato PDF haz clic aquí.



Para ver correctamente este archivo necesitas el lector de Adobe.

Tarea 3 Mecánica de Sólidos

Tarea del tema de Factor de Seguridad:





Ejercicios 1.49 & 1.52

El conector AC es de acero con un esfuerzo normal último de 60 ksi y tiene una sección uniforme de ¼ x ½ pulg. Está conectado a un soporte en A y al elemento BCD en C por medio de pasadores de 3/8 pulg. Mientras que el elemento BCD está conectado a B por un pasador de 5/16 pulg. Todos los pasadores son de acero con un esfuerzo cortante último de 25 ksi y están sometidos a cortante simple. Si se desea un Factor de Seguridad de 3.25, halle a) la máxima carga P que puede aplicarse en D. Note que el conector AC no está reforzado alrededor de los agujeros de los pasadores. La estructura se muestra en la siguiente figura:

b) Ahora resuelva el problema anterior suponiendo que la estructura ha sido rediseñada para usar pasadores de 5/16 pulg en A, C y B sin otros cambios.





Ejercicios 1.50, 1.51 & 1.53


En la estructura de acero, mostrada en la siguiente figura, un pasador de 6mm de diámetro se utiliza en C y pasadores de 10mm tanto en B como en D:

El cortante último es de 150 MPa en todas las conexiones y el esfuerzo último normal en el conector BD es de 400 MPa. Si se desea un Factor de Seguridad de 3, Halle a) la mayor fuerza P que se puede aplicar en A (note que el conector BD no está reforzado alrededor de los agujeros de los pasadores). b) Ahora resuelva este mismo problema suponiendo que la estructura se ha rediseñado para utilizar pasadores de 12mm en B y D. Ningún otro cambio se ha hecho. c) Ahora resuelva este mismo problema suponiendo que se han cambiado los diámetros en los pasadores en B y D a 11.5mm y que ningún otro cambio se ha hecho.

Para descargar este archivo en formato PDF haz clic aquí.



Para ver correctamente este archivo necesitas el lector de Adobe.